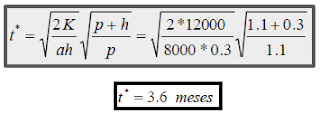TEORIA DE JUEGOS

TEORIA DE JUEGOS


La Teoría de Juegos fue creada por Von Neumann y Morgenstern, y descriptas en su libro clásico The Theory of Games Behavior, publicado en 1944. Otros habían anticipado algunas ideas. Los economistas Cournot y Edgeworth fueron particularmente innovadores en el siglo XIX. Otras contribuciones posteriores mencionadas fueron hechas por los matemáticos Borel y Zermelo. El mismo Von Neumann ya había puesto los fundamentos en el artículo publicado en 1928. Sin embargo, no fue hasta que apareció el libro de Von Neumann y Morgenstern que el mundo comprendió cuán potente era el instrumento descubierto para estudiar las relaciones humanas.

Von Neumann y Morgenstern investigaron dos planteamientos distintos de la Teoría de Juegos. El primero de ellos el planteamiento estratégico o no cooperativo. Von Neumann y Morgenstern resolvieron este problema en el caso particular de juegos con dos jugadores cuyos intereses son diametralmente opuestos. A estos juegos se les llama estrictamente competitivos, o de suma cero, porque cualquier ganancia para un jugador siempre se equilibra exactamente por una pérdida correspondiente para el otro jugador. El ajedrez, el backgammon y el póquer son juegos tratados habitualmente como juegos de suma cero. En el segundo de ellos desarrollaron el planteamiento coalicional o cooperativo, en el que buscaron describir la conducta óptima en juegos con muchos jugadores. Puesto que éste es un problema mucho más difícil, no es de sorprender que sus resultados fueran mucho menos precisos que los alcanzados para el caso de suma cero y dos jugadores. En particular, Von Neumann abandono todo intento de especificar estrategias óptimas para jugadores individuales. En lugar de ello se propuso clasificar los modelos de formación de coaliciones que son consistentes con conductas racionales.

La Teoría de Juegos actualmente tiene muchas aplicaciones, sin embargo, la economía es el principal cliente para las ideas producidas por los especialistas en Teoría de Juego. Entre las disciplinas donde hay aplicación de la Teoría de Juegos tenemos: La economía, la ciencia política, la biología y la filosofía.


Para ilustrar las características básicas de un modelo de teoría de juegos, considérese el juego llamado pares y nones. Éste consiste nada más en que los dos jugadores muestran al mismo tiempo uno o dos dedos. Si el número de dedos coincide, el jugador que apuesta a pares (por ejemplo, el jugador 1) gana la apuesta (digamos $l) al jugador que va por nones (jugador II). Si el número no coincide, el jugador 1 paga $l al jugador II.

Entonces, cada jugador tiene dos estrategias: mostrar uno o dos dedos. La tabla a continuación contiene el pago en dólares que resulta para el jugador 1 en una matriz de pagos.

Antes de iniciar el juego, cada jugador conoce las estrategias de que dispone, las que tiene su oponente y la matriz de pagos. Una jugada real en el juego consiste en que los dos jugadores elijan al mismo tiempo una estrategia sin saber cuál es la elección de su oponente.

Una estrategia puede constituir una acción sencilla, como mostrar un número par o non de dedos en el juego de pares y nones. Por otro lado, en juegos más complicados que llevan en sí una serie de movimientos, una estrategia es una regla predeterminad que especifica por completo cómo se intenta responder a cada circunstancia posible en cada etapa del juego. Por ejemplo, una estrategia de un jugador de ajedrez indica cómo hacer el siguiente movimiento para todas las posiciones posibles en el tablero, de manera que el número total de estrategias posibles sería astronómico.

Las aplicaciones de la teoría de juegos involucran situaciones competitivas mucho menos complicadas que el ajedrez pero las estrategias que se manejan pueden llegar a ser bastante complejas.


Por lo general, la matriz de pagos muestra la ganancia (positiva o negativa) que resultaría con cada combinación de estrategias para el jugador 1. Se da de esta manera, ya que la matriz del jugador II es el negativo de ésta, debido a la naturaleza de la suma cero del juego. Los elementos de la matriz pueden tener cualquier tipo de unidades, como dólares, siempre que representen con exactitud la utilidad del jugador 1 en el resultado correspondiente. Debe hacerse hincapié en que la utilidad no necesariamente es proporcional a la cantidad de dinero (o cualquier otro bien) cuando se manejan cantidades grandes. Por ejemplo, para una persona pobre $2 millones (después de impuestos) tal vez vale mucho más que el doble de $1 millón. En otras palabras, si a una persona se le da a elegir entre: 1) recibir, con el 50% de posibilidades, $2 millones en lugar de nada y 2) recibir $1 millón con seguridad, ese individuo tal vez prefiriera este último. Por otro lado, el resultado que corresponde a un elemento 2 en una matriz de pagos debe "valer el doble" para el jugador 1 que el resultado correspondiente a un elemento 1. Así, dada la elección, debe serle indiferente un 50% de posibilidades de recibir el primer resultado (en lugar de nada) y recibir en definitiva el último resultado.

Un objetivo primordial de la teoría de juegos es establecer criterios racionales para seleccionar una estrategia, los cuales implican dos suposiciones importantes:


1. Ambos jugadores son racionales.
2. Ambos jugadores eligen sus estrategias sólo para promover su propio bienestar (sin compasión para el oponente).

CADENAS DE MARKOV

CADENAS DE MARKOV


En la teoría de la probabilidad, se conoce como cadena de Markov a un tipo especial de proceso estocástico discreto en el que la probabilidad de que ocurra un evento depende del evento inmediatamente anterior. En efecto, las cadenas de este tipo tienen memoria. "Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Markov de las series de eventos independientes, como tirar una moneda al aire o un dado.
Reciben su nombre del matemático ruso Andrei Andreevitch Markov (1856-1922), que las introdujo en 1907.1
Estos modelos muestran una estructura de dependencia simple, pero muy útil en muchas aplicaciones.
En matemáticas, se define como un proceso estocástico discreto que cumple con la propiedad de Markov, es decir, si se conoce la historia del sistema hasta su instante actual, su estado presente resume toda la información relevante para describir en probabilidad su estado futuro.
Andrei Andréyevich Markov (14 de junio de 1856 - 20 de julio de 1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades.
Markov nació en Riazán, Rusia. Antes de los 10 años su padre, un funcionario estatal, fue trasladado a San Petersburgo donde Andrei entró a estudiar en un instituto de la ciudad. Desde el principio mostró cierto talento para las matemáticas y cuando se graduó en 1874 ya conocía a varios matemáticos de la Universidad de San Petersburgo, donde ingresó tras su graduación. En la Universidad fue discípulo de Chebyshov y tras realizar sus tesis de maestría y doctorado, en 1886 accedió como adjunto a la Academia de Ciencias de San Petersburgo a propuesta del propio Chebyshov. Diez años después Markov había ganado el puesto de académico regular. Desde 1880, tras defender su tesis de maestría, Markov impartió clases en la Universidad y, cuando el propio Chebyshov dejó la Universidad tres años después, fue Markov quien le sustituyó en los cursos de teoría de la probabilidad. En 1905, tras 25 años de actividad académica, Markov se retiró definitivamente de la Universidad, aunque siguió impartiendo algunos cursos sobre teoría de la probabilidad.
A parte de su perfil académico, Andrei Markov fue un convencido activista político. Se opuso a los privilegios de la nobleza zarista y llegó a rechazar las condecoraciones del propio zar en protesta por algunas decisiones políticas relacionadas con la Academia de Ciencias. Hasta tal punto llegó su implicación en la política que llegó a ser conocido con el sobrenombre de "el académico militante".
Markov arrastró durante toda su vida problemas relacionados con una malformación congénita en la rodilla que le llevaría varias veces al quirófano y que, con el tiempo, fue la causa de su muerte cuando el 20 de julio del año 1922 una de las muchas operaciones a las que se sometió le produjo una infección generalizada de la que no pudo recuperarse.
Aunque Markov influyó sobre diversos campos de las matemáticas, por ejemplo en sus trabajos sobre fracciones continuas, la historia le recordará principalmente por sus resultados relacionados con la teoría de la probabilidad. En 1887 completó la prueba que permitía generalizar el teorema central del límite y que ya había avanzado Chebyshov. Pero su aportación más conocida es otra.
Su trabajo teórico en el campo de los procesos en los que están involucrados componentes aleatorios (procesos estocásticos) darían fruto en un instrumento matemático que actualmente se conoce como cadena de Markov: secuencias de valores de una variable aleatoria en las que el valor de la variable en el futuro depende del valor de la variable en el presente, pero es independiente de la historia de dicha variable. Las cadenas de Markov, hoy día, se consideran una herramienta esencial en disciplinas como la economía, la ingeniería, la investigación de operaciones y muchas otras.

La teoría de juegos es un área de la matemática aplicada que utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados juegos) y llevar a cabo procesos de decisión. Sus investigadores estudian las estrategias óptimas así como el comportamiento previsto y observado de individuos en juegos. Tipos de interacción aparentemente distintos pueden, en realidad, presentar estructura de incentivo similar y, por lo tanto, se puede representar mil veces conjuntamente un mismo juego.
Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, como en la biología, sociología, psicología y filosofía. Experimentó un crecimiento sustancial y se formalizó por primera vez a partir de los trabajos de John von Neumann y Oskar Morgenstern, antes y durante la Guerra Fría, debido sobre todo a su aplicación a la estrategia militar —en particular a causa del concepto de destrucción mutua garantizada. Desde los setenta, la teoría de juegos se ha aplicado a la conducta animal, incluyendo el desarrollo de las especies por la selección natural. A raíz de juegos como el dilema del prisionero, en los que el egoísmo generalizado perjudica a los jugadores, la teoría de juegos ha atraído también la atención de los investigadores en informática, usándose en inteligencia artificial y cibernética.

MODELO EOQ CON DESCUENTO POR CANTIDAD

MODELO EOQ CON DESCUENTO POR CANTIDAD


Este modelo se basa manejar diferentes costos según las unidades pedidas, es decir, la cantidad de productos a comprar definirá el precio de los mismos. En este caso, la variable crítica de decisión es el costo unitario, ya que el costo de pedir y el costo de mantener en inventario permanecen constantes sin importar la cantidad a pedir.

Las empresas manejan este modelo de inventario debido a que sus costos le permiten realizar este tipo de compras, que generan una reducción del precio de venta en el producto fabricado, o un ahorro para la empresa. Este modelo les proporciona sus costos totales más bajos según sus necesidades y los recursos con los que cuenten. En la siguiente gráfica se representa este modelo.

MODELO LEP CON FALTANTE

MODELO LEP CON FALTANTE

Las suposiciones para este modelo son las siguientes:
1. La demanda se efectúa a tasa constante.
2. El reemplazo es instantáneo (la tasa de reemplazo es infinita).
3. Todos los coeficientes de costos son constantes.
4. La tasa de manufacturación es mayor que la tasa de demanda

Donde:
t4 = Tiempo en el cual la producción se nivela con los pedidos pendientes.
t1= Tiempo de producción en el que no hay faltantes y se llega al inventario máximo.
t2= Tiempo que transcurre para que el inventario máximo llegue a cero.
t3= Tiempo en el que se empiezan a acumular los pedidos, es decir, hay faltantes.

Definamos entonces los costos:
Cmi: Es el costo de mantener una unidad en inventario.
Cu: Costo unitario del producto.
Cop: Costo de orden de producción.
Cf: Costo por mercancía faltante.

MODELO LEP SIN FALTANTE

MODELO LEP SIN FALTANTE


El modelo LEP (Lote económico de producción) o cantidad económica de pedido es un modelo de inventario en el que partimos de la premisa de que producimos nuestra mercancía de inventario. Este parte de los siguientes supuestos:

 La demanda es constante y es conocida.
 No se admiten faltantes. Es decir, siempre se va a suplir la demanda del cliente con la cantidad requerida por este.
 Producimos a una tasa R y esta siempre es mayor que la demanda d periodica.
 Existen costos tanto de almacenamiento como costo de producción.
 Los costos se mantienen constantes.
 La reposición en el inventario es instantánea, ya que se plantea que no hay un tiempo de demora por pedidos, y que además, la cantidad de reaprovisión es la correcta (es decir, igual a la solicitada).

Definamos entonces los costos:

 Cmi: Es el costo de mantener una unidad en inventario.
 Cop: Costo de producción.
 Cu: Costo unitario de producto.

Si queremos hallar el valor de Q óptimo (Q*) con el que los costos Cmi y Cop se equilibren, es necesario derivar la ecuación anterior respecto a Q, y se iguala a 0 y se despeja Q. este proceso es analógico con el hallar máximos y mínimos de una función.

Si queremos hallar N* y t*, simplemente usamos las siguientes ecuaciones reemplazando Q por Q*.

MODELO EOQ CON FALTANTE

MODELO EOQ CON FALTANTE


Es normal que ocurran pequeños faltantes cuando por ahorrar dinero en el tiempo de preparación se pida un lote que no alcance para cubrir todo el ciclo.
Sin embargo también existirá un costo asociado a los faltantes, que llevará a que éstos no sean excesivos.
Los costos que se consideran son.
K = Costo de preparación para producir u ordenar un lote.
c = El costo de producir o comprar cada unidad.
h = El costo de mantenimiento de una unidad de inventario por unidad de tiempo.
P = El costo del faltante por una unidad de demanda insatisfecha por unidad de tiempo.

Debemos hallar el costo total por unidad de tiempo ($/tiempo)
Primero hallaremos los costos únicamente para un ciclo, por lo que los costos estarán en pesos ($).

Sabemos que el inventario positivo promedio es (S/2).

Para hallar el costo en un ciclo debemos multiplicar por el tiempo que demora en agotarse el inventario, es decir S/a.

Sabemos que el inventario negativo promedio es (Q-S)/2

Para hallar el costo en un ciclo debemos multiplicar por el tiempo que demora agotado el inventario, es decir (Q-S)/a

Entonces el costo total por ciclo es:

Para hallar el costo toral por unidad de tiempo basta dividir por Q/a

Este modo tiene 2 variables de decisión (S y Q) y los valores óptimos (S* y Q*) se encuentran estableciendo las derivadas parciales:

Ejemplo:
Manufactura para bocinas de televisores.
1. Cada vez que se produce un lote, se incurre en un costo de preparación de $12000.
2. El costo unitario de producción de una sola bocina (excluyendo el costo de preparación) es de $10 y es independiente del tamaño del lote fabricado.
3. El costo de mantenimiento de una bocina en almacén es de $0.3 por mes.
4. La demanda es de 8000 bocinas mensuales.
5. Cada bocina que falta cuando se necesita cuesta $1.10 por mes.

MODELO EOQ SIN FALTANTE

MODELO DE COMPRA SIN DEFICIT (EOQ SIN FALTANTE)

Este modelo considera los siguientes supuestos:

La demanda se conoce con certidumbre y los artículos salen a una tasa constante denotada por a.
El tiempo de adelanto es cero.
Se utiliza la política de punto de pedido.
El inventario se reabastece cuando llega a cero. No hay inventario de seguridad ni agotamientos.
El reabastecimiento es instantáneo.
La cantidad a pedir es constante.
Los costos no varían con el tiempo.

Los únicos costos que se consideran son:

K = Costo de preparación para producir u ordenar un lote.
c = El costo de producir o comprar cada unidad.
h = El costo de mantenimiento de una unidad de inventario por unidad de tiempo.

El objetivo consiste en determinar con qué frecuencia y en qué cantidad reabastecer el inventario, de manera que se minimice la suma de estos costos por unidad de tiempo.

Debemos hallar el costo total por unidad de tiempo ($/tiempo)
Primero hallaremos los costos únicamente para un ciclo, por lo que los costos estarán en pesos ($).

Sabemos que el inventario promedio es (Q/2)

Para hallar el costo en un ciclo debemos multiplicar por el tiempo que demora un ciclo, es decir Q/ a

Entonces el costo total por ciclo es:

Para hallar el costo total por unidad de tiempo basta dividir por Q/ a

Para hallar el costo mínimo basta con aplicar los conceptos básicos del cálculo. Derivamos la función anterior con respecto a Q y la igualamos a cero.

La derivada de la función costo total es:

Igualando a cero y despejando obtenemos la cantidad económica a ordenar o producir:

De manera similar obtenemos el tiempo óptimo:

Si no se consideran los costos por producir o comprar cada unidad obtenemos el costo de administración de los inventarios:

Ejemplo:
Manufactura de bocinas para televisores.
Una compañía que fabrica televisores produce sus propias bocinas para usarlas en la fabricación de los aparatos. Hay una demanda de 8000 televisores por mes y se necesita 1 bocina por televisor.
 Las bocinas se producen en lotes.
 Las bocinas se colocan en inventario hasta que se necesitan para ensamblarlas.
 La compañía está interesada en determinar cuándo y cuántas bocinas producir.
1. Cada vez que se produce un lote, se incurre en un costo de preparación de $12000.
2. El costo unitario de producción de una sola bocina (excluyendo el costo de preparación) es de $10 y es independiente del tamaño del lote fabricado.
3. El costo de mantenimiento de una bocina en almacén es de $0.3 por mes.

Esta respuesta nos indica que la solución óptima es hacer una preparación de la línea de producción de bocinas cada 3.2 meses y producir 25298 bocinas cada vez.

Costo total por unidad de tiempo = $87589/mes.